数理工学研究グループ
citius, accuratior, robustior, elegantior
極めて大きな自由度をもつ自然系や人工物系の振る舞いを理解し,予測するため,既知の基礎法則や支配原理から出発した計算機による大規模計算が不可欠です.近年,科学技術計算の進歩はめざましく,その内容は高速計算機の出現によるものだけではなく計算アルゴリズムの驚異的な進歩によるものであり,計算機が速くなればなるほど数値計算アルゴリズムの速さがますます重要になるといえます.
そこで,本グループでは数値解析学・応用数学の基礎理論に基づいて「より速く,より高精度,よりロバストに,よりエレガントに」をキャッチコピーとして高性能計算アルゴリズムの開発に関する研究を行ない,それらを用いて物理・工学的諸問題に対する計算機上での数値的な解明に寄与します.
代数系
数値線形代数
物理・工学的に需要の高い以下の方程式に対する高性能計算アルゴリズムの開発を行っています.
・線形方程式: \(A\boldsymbol{x} =\boldsymbol{b}\)(応用例:流体,構造解析)
・固有値問題: \(A\boldsymbol{x} =\lambda \boldsymbol{x}\)(応用例:物性物理)
・特異値問題: \(A=U\Sigma V^\top\) (応用例:データ分析)
数値多重線形代数
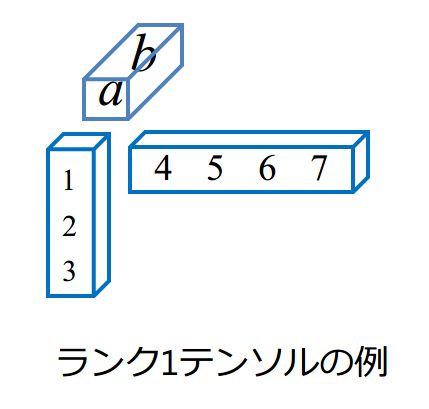
物理に現れる偏微分方程式を離散化する際に現れる線形方程式の安定性を調べる際に,テンソル空間 視点から効率の良い計算手法の開発を行っています.実は,デジタルカラー画像もテンソルとしてみることができますので,テンソルの視点の奥深さ(身近さ)が分かると思います.
行列関数・行列方程式

平方根は中学校で学ぶ概念ですが,行列の平方根の概念は大学でも明確には学ばないと思います.(ただし,量子力学・量子情報科学で目にしたことはあるかもしれません.)そこで,行列関数計算に対する高速・高精度化を研究しています.さらに一般に,\(F\)を行列値関数とした行列方程式\(F(X)=O\)の解\(X\)(行列)を求める数値計算法の開発にも取り組んでいます.
解析系
有限要素法の基礎理論
微分方程式の数値計算手法として, 最も単純なものは, 微分を差分で近似する, 差分法と呼ばれる手法です. しかし, 差分法は領域の形に制限が強く, 汎用的であるとは言えません. それに対して, 有限要素法と呼ばれる, 変分法的な定式化に基づく数値計算手法は, 領域の形の自由度が非常に高いため, 多くの分野で利用されています. 有限要素法は数学理論との相性が非常に高いため, 誤差評価などの理論解析の成果が数多く知られているのですが, それでも未解決問題は多く存在します. 本グループでは, 有限要素法の基礎理論を研究しています.
界面現象に対する数値解析
コップの中で水と油を混ぜると, 混ざることなく分離します. このとき, 水と油の境界面 (これを界面と呼びます) は, さまざまな運動をします. このような界面現象は, 水と油に限らず, 物理学や生物学において数多く現れます. また, これらの運動は微分方程式として数学モデル化され, 世界中で研究されています. 界面問題を記述する微分方程式は, 自然現象だけでなく, 画像処理にも応用できることが知られています. 本グループでは, これらの方程式に対して, 様々な角度から数値解析を行っています.
幾何学的数値解法(構造保存数値解法)
微分方程式の数値解法にはルンゲ・クッタ法などの多くの汎用解法が知られています.しかし,汎用解法では不十分な問題も多いため,それらに対応すべく,微分方程式の数理構造(例えばエネルギー保存則)に着目して,新しいタイプの数値解法—構造保存数値解法−の開発を行っています.これらは,汎用解法よりも高速,高精度,ロバスト,エレガントであり,また,天文学から分子動力学,流体計算に至るまで物理の様々な分野に貢献します.
微分方程式の数値計算のための数値線形代数
微分方程式の数値計算は,離散化後は線形方程式を解くことに帰着されます.本グループでは,従来型の「離散化後は数値線形代数の研究者におまかせ」するスタンスではなく,代数系と解析系が密接に連携することで,より効率的な数値解法を開発しています.
連続最適化・離散最適化・その他
ある条件のもとで利益(損失)を最大(最小)にするという最適化問題は,物理・工学だけでなく高度情報化社会のあらゆる場面で重要です.本グループでは,例えば以下のようなテーマにも取り組んでいます.
・圧縮センシング
・球面制約上の最適化問題
・関数同定問題(Parse-Matrix Evolution,遺伝的アルゴリズム)
・ビッグデータ
・データ同化
・不確実性を考慮した数値解法
アルゴリズム関係で何かやりたいと思う方はぜひ張研究室に相談に来てください。
工学部3号館南館481号室 張 教授
工学部3号館南館479号室 曽我部 准教授
工学部3号館南館483号室 剱持 助教